数位 DP

简介

给定区间 [L, R]，求该区间中符合某种条件的数的个数

与数的大小无关，与数的每一位的组成有关
本质：搜索 + 记忆化
用 f[n] 记录 [0, n] 之间满足条件的书的个数，结果：f[R] - f[L - 1]

HDU 2089 · 不要 62

Description

给定两个数 L, R，计算 [L, R] 中数位上没有出现 4 或 62（连续）的数的个数

Solution

求符合条件的数的个数

int dp[10][10];    //dp[x][y]：长度为 x，首位为 y 的数中符合条件的个数
dp[0][0] = 1;
for (int l = 1; l <= 7; l++)
{
    for (int i = 0; i <= 9; i++)
    {
        if (i == 4) dp[l][i] = 0;
        else
        {
            for (int j = 0; j <= 9; j++)
            {
                if (i == 6 && j == 2) continue;
                else
                {
                    dp[l][i] += dp[l - 1][j];
                }
            }
        }
    }
}

求 [0, n] 中符合条件的数的个数
设 n = 234
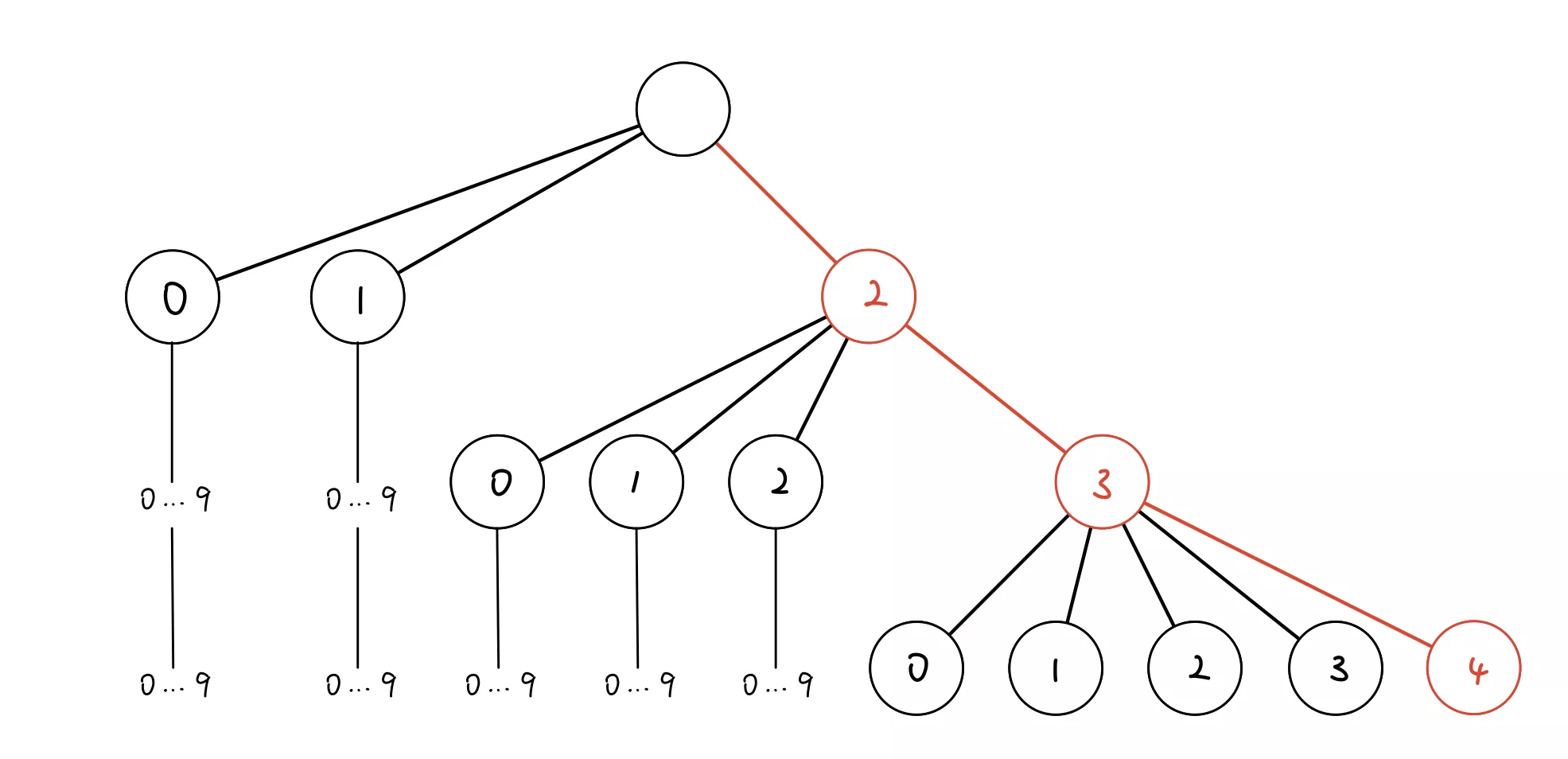
显然答案不是 dp[3][2]，因为三位数以 2 开头的数中包含 235 等大于 234 的数
因此要按如下分段求：
- dp[3][0] + dp[3][1] 求出三位数中 0xx, 1xx
- dp[2][0] + dp[2][1] + dp[2][2] 求出两位数中 0x, 1x, 2x
- dp[1][0] + dp[1][1] + dp[1][2] + dp[1][3] 求出一位数中 0, 1, 2, 3
但是假如分段中含 4 或者 62 的，如 345，则遇到 4 或 62 就停止，因为
继续细分出的段的高位肯定包含了 4 或 62
- dp[3][0] + dp[3][1] + dp[3][2] 求出三位数中 0xx, 1xx, 2xx
- dp[2][0] + dp[2][1] + dp[2][2] + dp[2][3] 求出两位数中 0x, 1x, 2x, 3x

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <cctype>
#include <algorithm>
#include <iostream>
#include <queue>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <list>
using namespace std;

int m, n;
int dp[10][10];
int d[10];

void Init()
{
    dp[0][0] = 1;
    for (int l = 1; l <= 7; l++)
    {
        for (int i = 0; i <= 9; i++)
        {
            if (i == 4) dp[l][i] = 0;
            else
            {
                for (int j = 0; j <= 9; j++)
                {
                    if (i == 6 && j == 2) continue;
                    else
                    {
                        dp[l][i] += dp[l - 1][j];
                    }
                }
            }
        }
    }
}

int get(int n)
{
    int ans = 0;
    int len = 0;
    while (n)
    {
        ++len;
        d[len] = n % 10;
        n /= 10;
    }
    d[len + 1] = 0;
    for (int i = len; i >= 1; --i)
    {
        for (int j = 0; j < d[i]; ++j)
        {
            if (d[i + 1] != 6 || j != 2)
                ans += dp[i][j];
        }
        if (d[i] == 4 || (d[i + 1] == 6 && d[i] == 2))
            break;
    }
    return ans;
}

int main()
{
    Init();
    
    while (1)
    {
        scanf("%d%d", &m, &n);
        if (!n && !m) return 0;
        printf("%d\n", get(n + 1) - get(m));
    }
    
    
    return 0;
    
}

SCOI 2009 · Windy 数

Description

给定一个区间 [L, R]，求其中满足条件不含前导 0 且相邻两个数字相差至少为 2 的数字个数。

Accepted Code

#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <cctype>
#include <algorithm>
#include <iostream>
#include <queue>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <list>
using namespace std;

int dp[11][11];
int a[11], p, q;

void Init()
{
    for (int i = 0; i <= 9; i++) dp[1][i] = 1;
    for (int l = 2; l <= 10; l++)
    {
        for (int i = 0; i <= 9; i++)
        {
            for (int j = 0; j <= 9; j++)
            {
                if (abs(i - j) >= 2) dp[l][i] += dp[l - 1][j];
            }
        }
    }
}

int work(int x)    //计算 <=x 的 windy 数 
{
    memset(a, 0, sizeof(a));
    int len = 0, ans = 0;
    while (x)
    {
        a[++len] = x % 10;
        x /= 10;
    }
    //分为几个板块 先求 len - 1 位的 windy 数 必定包含在区间里的 
    for (int i = 1; i <= len - 1; i++)
    {
        for (int j = 1; j <= 9; j++)
        {
            ans += dp[i][j];
        }
    }
    //然后是 len 位 但最高位 < a[len] 的 windy 数 也包含在区间里 
    for (int i = 1; i < a[len]; i++)
    {
        ans += dp[len][i];
    }
    //接着是 len 位 最高位与原数相同的 最难搞的一部分 
    for (int i = len - 1; i >= 1; i--)
    {
        //i 从最高位后开始枚举 
        for (int j = 0; j <= a[i] - 1; j++)
        {
            //j 是 i 位上的数 
            if (abs(j - a[i + 1]) >= 2)    ans += dp[i][j]; //判断和上一位 (i + 1) 相差 2 以上
               //如果是 ans 就累加 
        }
        if (abs(a[i + 1] - a[i]) < 2) break;
        //  if(i == 1)   ans += 1;
    }
    return ans;
}

int main()
{
    Init();
    cin >> p >> q;
    cout << work(q + 1) - work(p) << endl;
    return 0;
}