线段树
线段树
问题引入
假设需要反复对一个数组 a[] 进行以下两个操作:
Query · 求和
对 a[l] ~ a[r] 求和
Update · 修改
将 a[idx] 的值修改为 val
则有如下解决办法:
朴素做法
Build
for (int i = 1; i <= n; i++) scanf ("%d", &a[i]);Query
for (int i = l; i <= r; i++) sum += a[i];O(n)Update
a[idx] = val;O(1)
前缀和
Build
for (int i = 1; i <= l; i++) { scanf ("%d", &a[i]); sum_a[i] = sum_a[i-1] + a[i]; }Query
sum = sum_a[r] - sum_a[l - 1];O(1)Update
for (int i = idx; i <= n; i++) sum_a[i] += val;O(n)
可见,两种方法的时间复杂度都较高,于是引入线段树的数据结构
定义
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
——百度百科
Build
如图,区间依次对半分,每个节点存储一部分区间的和,节点按序标记为 1 ~ n(图中为 0 ~ n - 1)
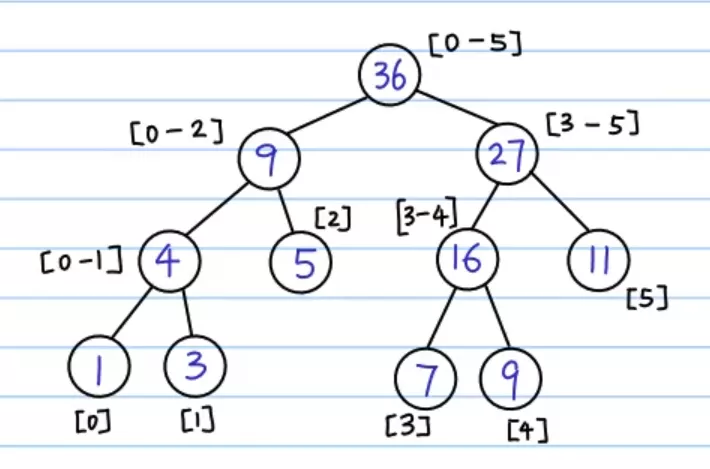
Query
O(logn)- 从根结点开始划分求和区间
- 如果节点区间为求和区间的子集:返回节点值
- 如果节点区间与求和区间无交集:返回 0
Update
O(logn)- 找到修改的节点,修改值
- 向上更新节点值
模板 · 单点修改 · 数组
/*
输入数据个数 n
一行输入 n 个数据
输入修改个数 m
m 行每行修改下标 idx 及修改数据 val
输入查询个数 q
q 行每行查询左边界右边界 l r
*/
#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
const int MAX_LEN = 1000016;
int n, m, q;
struct SEGT
{
int arr[MAX_LEN], tree[MAX_LEN << 2];
void build_tree(int node, int start, int end)
{
if (start == end)
{
tree[node] = arr[start];
return;
}
int mid = (start + end) >> 1;
int left_node = node << 1;
int right_node = node << 1 | 1;
build_tree(left_node, start, mid);
build_tree(right_node, mid + 1, end);
tree[node] = tree[left_node] + tree[right_node];
}
void update_tree(int node, int start, int end, int idx, int val)
{
if (start == end)
{
arr[idx] = val;
tree[node] = arr[idx];
return;
}
int mid = (start + end) >> 1;
int left_node = node << 1;
int right_node = node << 1 | 1;
if (idx <= mid)
update_tree(left_node, start, mid, idx, val);
else
update_tree(right_node, mid + 1, end, idx, val);
tree[node] = tree[left_node] + tree[right_node];
}
int query_tree(int node, int start, int end, int l, int r)
{
if (r < start || l > end) return 0;
if (l <= start && r >= end) return tree[node];
if (start == end) return tree[node];
int mid = (start + end) >> 1;
int left_node = node << 1;
int right_node = node << 1 | 1;
int sum_left = query_tree(left_node, start, mid, l, r);
int sum_right = query_tree(right_node, mid + 1, end, l, r);
return sum_left + sum_right;
}
};
SEGT segt;
int main()
{
while (scanf("%d", &n) != EOF)
{
for (int i = 1; i <= n; i++) scanf("%d", &segt.arr[i]);
segt.build_tree(1, 1, n);
scanf("%d", &m);
while (m--)
{
int idx, val;
scanf("%d%d", &idx, &val);
segt.update_tree(1, 1, n, idx, val);
}
scanf("%d", &q);
while (q--)
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", segt.query_tree(1, 1, n, l, r));
}
}
return 0;
}模板 · 区间修改
模板 · 权值线段树
#define _CRTSECURE_NOWARNINGS
#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<set>
#include<list>
using namespace std;
int n, m, p;
int a[10001];
int arr[10001]; //arr[x]表示数 x 有多少个
int tree[10001];
void build_tree(int node, int l, int r)
{
int mid = (l + r) / 2;
if (l == r)
{
tree[node] = arr[l];
return;
}
int left_node = node * 2;
int right_node = node * 2 + 1;
build_tree(left_node, l, mid);
build_tree(right_node, mid + 1, r);
tree[node] = tree[left_node] + tree[right_node];
}
void update_tree(int node, int l, int r, int k, int cnt) //表示数k的个数多cnt个
{
int mid = (l + r) / 2;
if (l == r)
{
tree[node] += cnt;
return;
}
int left_node = node * 2;
int right_node = node * 2 + 1;
if (k <= mid)
update_tree(left_node, l, mid, k, cnt);
else
update_tree(right_node, mid + 1, r, k, cnt);
tree[node] = tree[left_node] + tree[right_node];
}
int query_tree(int node, int l, int r, int k) //查询数k有多少个
{
int mid = (l + r) / 2;
if (l == r)
return tree[node];
int left_node = node * 2;
int right_node = node * 2 + 1;
if (k <= mid)
return query_tree(left_node, l, mid, k);
else
return query_tree(right_node, mid + 1, r, k);
}
int kth_tree(int node, int l, int r, int k) //查询第k大值是多少
{
int mid = (l + r) / 2;
if (l == r)
return l;
int left_node = node * 2;
int right_node = node * 2 + 1;
int s1 = tree[left_node];
int s2 = tree[right_node];
if (k <= s2)
return kth_tree(right_node, mid + 1, r, k);
else
return kth_tree(left_node, l, mid, k - s2);
}
int main()
{
freopen("in.txt", "r", stdin);
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
arr[a[i]]++;
}
scanf("%d%d", &m, &p);
build_tree(1, 1, m);
printf("%d", kth_tree(1, 1, m, p));
return 0;
}