并查集
并查集
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。常常在使用中以森林来表示。
——百度百科
主要操作
初始化
int f[N]; void Init(int x) { for (int i = 1; i <= x; i++) f[i] = i; }使所有元素都指向自己,将自己作为父节点
查找
int Find(int x) { if (x == f[x]) return x; return Find(x); }合并
void Merge(int x, int y) { f[Find(x)] = Find(y); }
优化
路径压缩
每次查找的时候,如果路径较长,则修改信息,以便下次查找的时候速度更快。
第一步,找到根结点。
第二步,修改查找路径上的所有节点,将它们都指向根结点。
——百度百科
查找
int Find(int x) { if (x == f[x]) return x; f[x] = Find (f[x]); return f[x]; }或者写成这样:
int Find(int x) { if (x != f[x]) f[x] = Find (f[x]); return f[x]; }再用二元运算符:
int Find(int x) { return x == f[x] ? x : (f[x] = Find(f[x])); }这么写可以让自己看起来更加大佬
按秩合并
将深度小的树合并到深度大的树上
初始化
void Init(int x) { for (int i = 1; i <= x; i++) { f[i] = i; rank[i] = 1; //深度都初始化为1 } }合并
void Merge(int x, int y) { int a = Find(x), b = Find(y); //先找到两个根节点 if (rank[a] <= rank[b]) f[a] = b; else fa[b] = a; if (rank[a] == rank[b] && a != b) rank[b]++; //如果深度相同且根节点不同,则新的根节点的深度+1 }因为是小的直接连接到大的根节点,所以合并时小的那一支的深度+1,只有当两者深度相同时才会产生更大的深度
拓展
种族并查集
通过多个并查集将不同的元素归类,并维护相互之间的关系
例题:洛谷 P2024 食物链
用三个并查集分别表示自己、自己的猎物(自己吃的)以及自己的天敌(吃自己的),同时维护三个并查集,通过他们三者的关系判断当前读入数据是否为真
带权并查集
基于路径压缩,每个节点都记录的是与根节点之间的权值
查找
int Find(int x) { if (x != f[x]) { int t = f[x]; f[x] = Find(f[x]); value[x] += value[t]; } return f[x]; }合并
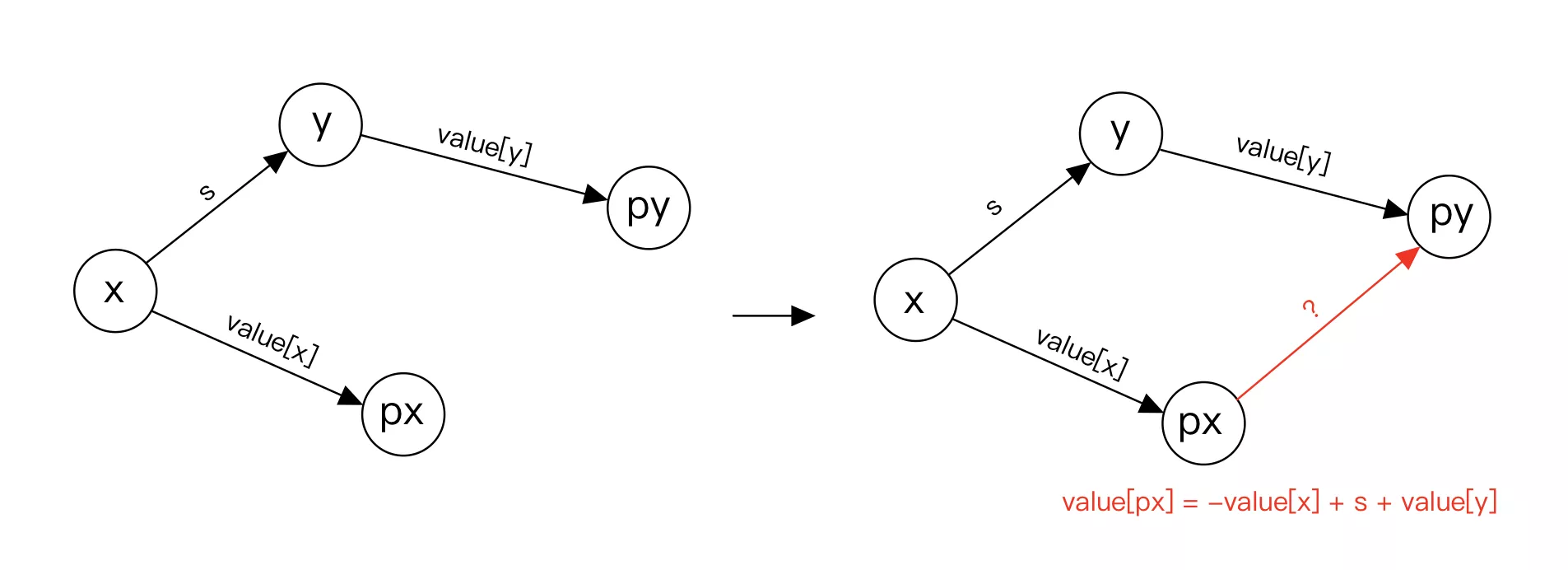
void Merge(int x, int y) { int px = Find(x); int py = Find(y); if (px != py) { f[px] = py; value[px] = -value[x] + value[y] + s; } }